Have you ever felt that one same thing, can have various different meanings in different points of your life? For example, I used to dislike Apple products, due to their closed architecture, lack of customization, all the related Steve Jobs fanboys etc. Now my opinion has shifted, and I am considering purchasing a macbook pro.
This paper: "From Amateurs to Connoisseurs: Modeling the Evolution of User Expertise through Online Reviews" from www2013, models precisely how users' perceptions on products (particularly beer!) change through time. Note that perceptions can be compared to level of expertise.
The work considers that users evolve on their own "personal clock" (i.e., each user is modelled on its own time-scale.) so some users may be really experienced when they provide their first review, while other users may never ever become experts. It is also assumed, that users with similar levels of expertise will rate products in similar ways, even if their ratings are temporally far apart, e.g., a user from 2013 will rate things similarly to a user from 1999, if both users are in the same "noob level" (note that what will remain constant throughout time is what the "noob level" means.)
The work models the level of experience of each user as a series of latent parameters that are constrained to be monotonically non-decreasing as a function of time. Therefore users can only become more experienced (or stay at least at the same level of experience...this clearly does not consider cases related to the German word of "Verlernen," where you forget something you have already learned!) Users evolve as they rate more products, i.e. the work considers that the very act of consuming products will cause users' tastes to change.
In particular the authors consider that users move from one level of expertise to another, depending on how they rate particular products. Given that the paper works with a beer rating dataset, the authors consider that expert users will rate higher the hoppiest beers, i.e. the strong Ales (confused what hops in beer mean, check this article out.) It is assumed that liking strong Ales is an acquired taste.
The figure below shows the ratings different users have given to different beers. We see how the Firestone XV, a strong ale, is one of the beer that was rated the highest, and they consider this corresponds to an expert rating. The figure also shows how biases can exist for different beers given the level of expertise of the user.
The approach is somewhat simple, different recommender systems are created for different stages of user evolution.
A classic latent factor recommender system would look something like the following:
The authors create a sort of feature vector, that has different recommender systems for each stage of the user's life cycle:
Latent factor recommender models, are a collaborative filtering type recommendation algorithms, which consider that for specific domains (e.g., action films or beer) there exits a set of factors that influence the rating a specific item receives. These factors are not obvious, and it is difficult to predict the actual impact they have on a rating.
The first goal of the latent factor recommender models is to infer these latent factors from the data by using mathematical techniques.
In the author's approach it is considered that users that have a certain experience level will be influenced by certain type of factors in their rating. So e.g., a novice user the fact that a certain beer is more inexpensive than another might play a big role in how much the user says to like the beer, but for a more experiencied user, he might be more influenced by the beer's texture. This is why the authors consider different recommender models for each experience level of the user.
Latent Factor models map users and items into a latent feature space.
A user's feature vector denotes the user's affinity to each of the features. The product or item's feature vector represents how much the item itself is related to the features. A rating is approximated by the dot product of the user feature vector and the item feature vector.
Specifically, consider that we have a set
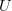 of users, and a set
of users, and a set 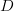 of items. Let
of items. Let 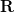 of size
of size 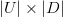 be the matrix that contains all the ratings that the users have given to the items.
be the matrix that contains all the ratings that the users have given to the items.The first task of this method is to discover the $K$ latent features. At the end of the day, we want to find two matrics matrices U (a
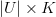 matrix) and M (a
matrix) and M (a 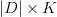 matrix) such that their product approximates
matrix) such that their product approximates 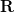 :
: The following image shows how the rating of items is composed of the dot product of matrices with these feature vectors:
Note that the M transposed matrix corresponds to the feature vectors of items.
Each row of U represents the strength of the associations between a user and the features. Similarly, each row of M represents the strength of the associations between an item and the features. To get the prediction of a rating of an item
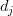 by
by 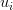 , we calculate the dot product of the two vectors corresponding to
, we calculate the dot product of the two vectors corresponding to 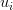 and
and 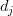 :
: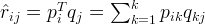
The task is now to obtain U and M. One common way to approach this problem is the first intialize the two matrices with some values, calculate how `different’ their product is to R, and then try to minimize this difference iteratively. This method is called gradient descent. Its purpose is find a local minimum of the difference.
This difference is usually called the error between the estimated rating and the real rating, can be calculated by the following equation for each user-item pair:
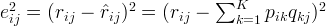
The squared error is considered because the estimated rating can be either higher or lower than the real rating.
To minimize the error, we need to know in which direction we have to modify the values of
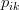 and
and 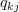 .
In other words, we need to know the gradient at the current values. Thus we differentiate the above equation with respect to these two
variables separately:
.
In other words, we need to know the gradient at the current values. Thus we differentiate the above equation with respect to these two
variables separately: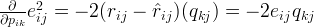
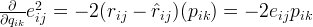
With the gradient, the update rules for both
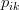 and
and 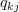 can be formulated as:
can be formulated as: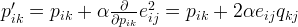
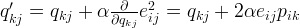
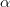 is a constant that helps determine the rate of approaching the minimum. Usually the value of
is a constant that helps determine the rate of approaching the minimum. Usually the value of 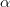 is small to avoid the risk of missing the minimum and oscillating around the minimum.
is small to avoid the risk of missing the minimum and oscillating around the minimum. Ok...
Now that latent factor models are clear (hopefully)...let's get back to the author's problem.
As we mentioned previously, the authors consider that for each evolution stage of a user, there will be a recommender system that can adequtly capture the user's taste at that point in his life.
So their problem comes down to:
-Fitting the parameters of their recommender system.
-Fit the user's experience progression (i.e., be able to state that when the author reviewed X item, they were at a certain experience rate.)
Note that once we know the experience level in which all users contributed each of their reviews, fitting the parameters of each recommender model is a snitch (it's basically the same procedure experienced for classic latent factor recommendations.)
The question now is, how do we fit the user's experience progression? Well if we assume that users gain experience monotonically, as they rate more products, we can fit experience using dynamic programming.
The two steps (fitting each user's experience level, and fitting the parameters of each recommender ) are repeated until conversion.





No comments:
Post a Comment